Difference between revisions of "3rd:Solution of Alphametic Puzzles"
Ferenc Nagy (talk | contribs) (Solution of Alphametic Puzzles) |
Ferenc Nagy (talk | contribs) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 5: | Line 5: | ||
You have to substitute same numbers for the same letters, different numbers for the different letters. | You have to substitute same numbers for the same letters, different numbers for the different letters. | ||
Their special forms are the [http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/ALPHAMETIC/alphametic-mike-keith.html#doub doubly true] puzzles. | Their special forms are the [http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/ALPHAMETIC/alphametic-mike-keith.html#doub doubly true] puzzles. | ||
A Hungarian example is | |||
---- | |||
TÍZ+TÍZ=HÚSZ | TÍZ+TÍZ=HÚSZ | ||
---- | |||
where the words for added numbers in a certain language form true sentence. | where the words for added numbers in a certain language form true sentence. | ||
TÍZ=ten in Hungarian, HÚSZ=twenty in Hungarian. | TÍZ=ten in Hungarian, HÚSZ=twenty in Hungarian. | ||
TEN=TEN=TWENTY has no solution in English. | TEN=TEN=TWENTY has no solution in English. | ||
---- | |||
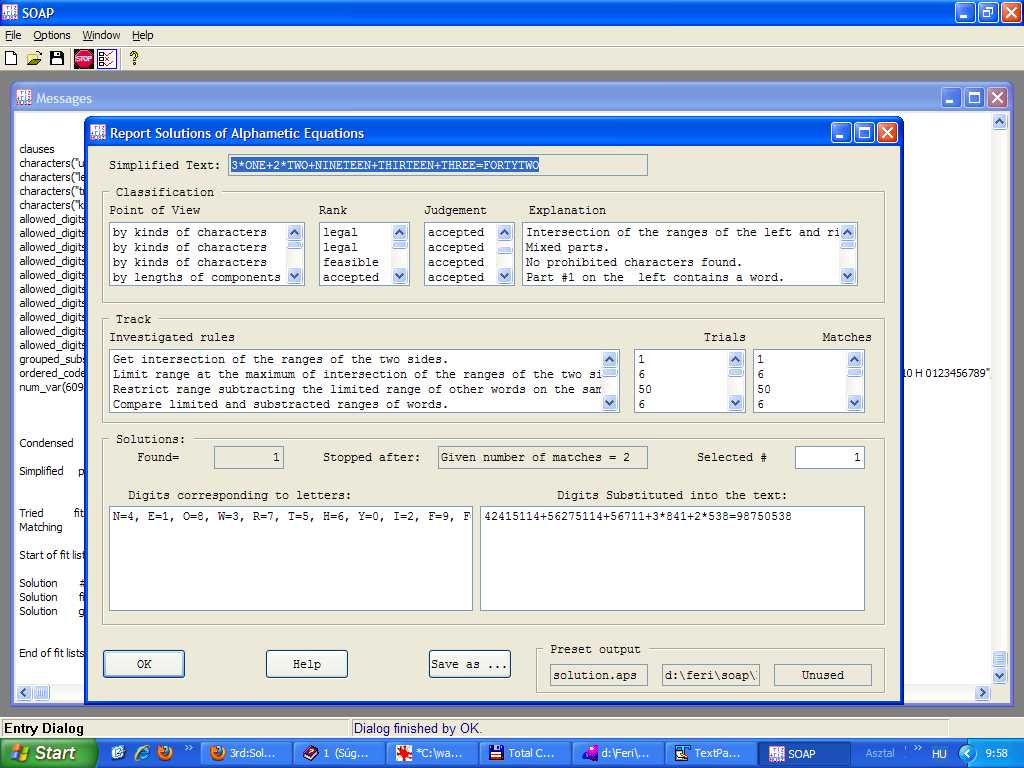
NINETEEN + THIRTEEN + THREE + 2*TWO+ 3*ONE = FORTYTWO | |||
---- | |||
is a more complicated English doubly true cryptarithm. | |||
German example: 2*SECHS=ZWOELF. | German example: 2*SECHS=ZWOELF. | ||
| Line 18: | Line 32: | ||
''I intended to follow the human way of the thinking instead of brute force full trial and error of all possible letter-digit matching. The program uses rules of divisibilty and comparision of mininal and maximal values of the left and right sides of the equations.'' | ''I intended to follow the human way of the thinking instead of brute force full trial and error of all possible letter-digit matching. The program uses rules of divisibilty and comparision of mininal and maximal values of the left and right sides of the equations.'' | ||
[[Image:Englishdoublytrue.jpg]] | |||
--[[User:Ferenc Nagy|Frank]] 09:38, 5 January 2011 (CET) | --[[User:Ferenc Nagy|Frank]] 09:38, 5 January 2011 (CET) | ||
Latest revision as of 10:01, 5 January 2011
The solution alphametic puzzles on my homepage The alphametic puzzles are the generalizations of the puzzles of type
SEND+MORE=MONEY
You have to substitute same numbers for the same letters, different numbers for the different letters. Their special forms are the doubly true puzzles. A Hungarian example is
TÍZ+TÍZ=HÚSZ
where the words for added numbers in a certain language form true sentence. TÍZ=ten in Hungarian, HÚSZ=twenty in Hungarian. TEN=TEN=TWENTY has no solution in English.
NINETEEN + THIRTEEN + THREE + 2*TWO+ 3*ONE = FORTYTWO
is a more complicated English doubly true cryptarithm.
German example: 2*SECHS=ZWOELF.
In order accept Russian puzzles the program accepts Unicode input and writes Unicode output.
Prolog version: VIP 7.2 PE.
The help file written using VAHELP
VAHELP Help Maker
I intended to follow the human way of the thinking instead of brute force full trial and error of all possible letter-digit matching. The program uses rules of divisibilty and comparision of mininal and maximal values of the left and right sides of the equations.
 --Frank 09:38, 5 January 2011 (CET)
--Frank 09:38, 5 January 2011 (CET)
